Sections:

Motion in One Dimension, Page 17

Equations of Motion

A freely falling object has zero velocity initially. How can its velocity be found after a certain time? To answer such questions/problems, one has to visualize the motion in a mathematical point of view. 

Consider an object moving under constant acceleration, a, and its velocity changes from vi to vf. 

We know, a = 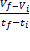V sub f - V sub i / t sub f - t sub i

Simplifying this equation, we get, 

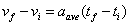V sub f - V sub i = A sub avg (t sub f - t sub i) -------------- I 

Another equation of motion can be derived by using the following velocity-time graph of constant acceleration. 

Velocity time graph of constant acceleration

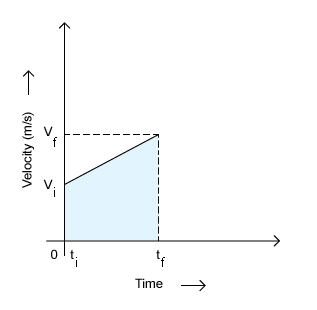
Area = area of a rectangle + area of a triangle 

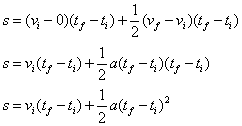s = (v sub i - 0)(t sub f - t sub i) + 1/2(v sub f - v sub i)(t sub f - t sub i); s = v sub i (t sub f - t sub i) + 1/2a(t sub f - t sub i)(t sub f - t sub i); s = v sub i(t sub f - t sub i) + 1/2a(t sub f - t sub i) squared----------II

Similarly, the third equation of motion can also be derived. 

The third equation of motion is, 

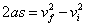 2as = v sub f squared - v sub i squared ---------------- (III) 

We call these as kinematics equations in physics. 

In all these kinematics equations, 

t sub f - t sub i = time interval; v sub f = final velocity; v sub i = initial velocity; a = uniform acceleration; s = displacement of the object in motion