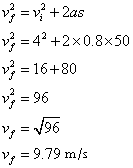Solved Problems using Kinematics Equations
- A car is initially moving with a velocity of 2 m/s. Then it accelerates uniformly at the rate of 0.4 m/s2 for 5 seconds. What is the distance covered by the car in 5 seconds?
Solution:
Given: initial velocity vi = 2 m/s, acceleration, a = 0.4 m/s2 and time, t = 5 seconds
The distance, s, can be calculated by using the following kinematic equation.
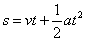
Substituting the values of v, a and t we get,
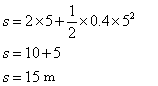
- A truck starts from rest and attains a velocity of 4 m/s in 3 seconds. What is its acceleration?
Solution:
Given: vi = 0, vf = 4 m/s and t = 3 seconds.
The acceleration can be found out by using the following kinematic equation.
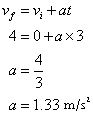
- A truck accelerates uniformly at the rate of 0.8 m/s2 for a distance of 50 m. If the truck started with an initial velocity of 4 m/s, what is its velocity at the end of 50 m?
Solution:
Given: a = 0.8 m/s2, s = 50 m and vi = 4 m/s
The velocity can be found out by using the following kinematic equation.
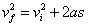
Substituting the values of a, s and vi we get,