Two Dimensional Motion and Vectors, Page 11

Projectile Motion-Projection at an Angle

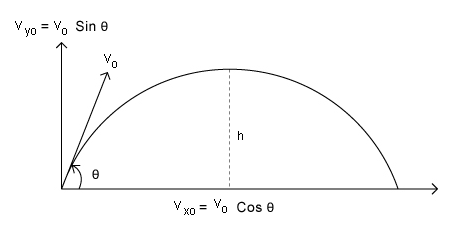
• When an object is launched with a velocity ‘v’ at an angle θ with respect to horizontal line as shown, then it has both an x-component of velocity (v_xo) and a y component of velocity (v_yo).
• v_xo and v_yo are the initial x and y components of velocity. v_xo = v_o cos θ and v_yo = v_o sin θ.
• v_xf and v_yf are the final x- and y-components of velocity. v_xf = v_x = v cos θ, since the x-component is not affected by any other force. v_y will not remain constant as v_x, because v_y is influenced by gravity. It can be found using the equations of motion as explained below.
• Kinematics equations for this kind of projectile motion are simplified as follows:

h = v_yot + (1/2)*g*t²
v_yf = v_yo + g * t

v²_yf = v²_yo + 2* g* h 

v_y = final velocity in the vertical direction
v_x = final velocity in the horizontal direction
h = vertical displacement in the downward direction

• You can find the horizontal distance (x), the range, of the projectile by using x = v_xo* t

While solving problems using the kinematics equations, the following sign conventions are followed:

1. Any vector quantity such as displacement, velocity etc. in upward direction is positive.
2. Any vector quantity such as displacement, velocity etc. in downward direction is negative, so acceleration due to gravity g is negative as it always acts in the downward direction.