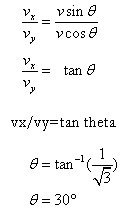Two Dimensional Motion and Vectors, Page 8

Solved Examples of Finding Vector Components

1. A baseball is hit with a velocity of 14 m/s at angle of 30° with the horizontal direction. What are the horizontal and vertical vector components of the velocity vector? 
   
   Solution: 
   
   Given: v = 14 m/s, horizontal component v_x = ? and the vertical component v_y = ?
   
   Since the velocity vector makes angle θ with the horizontal then

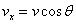
and 

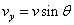
Substituting the values of V and θ = 30° we get,

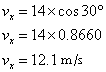
and the vertical component is 

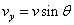
2. A bullet shot from the gun at an angle of 60°. Its horizontal component is 40 m/s. What is the actual velocity? 
   
   Solution: 
   
   Given: θ = 60°, v_x = 40 m/s and v = ?
   
   The horizontal component of the velocity.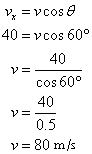 

   

3. The horizontal and vertical components of the velocity vector of the foot ball are 10√3m/s and 10 m/s respectively. What is the angle at which the ball is thrown? 
   
   Solution: 
   
   Given: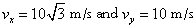
   
   We know,  and 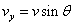. Dividing these two equations we get